いまさら、森博嗣のビリヤード問題を解く

大変いまさらですが、「笑わない数学者」（森博嗣）の中に出てくる「ビリヤード問題」を考えてみたいと思います。ビリヤード問題とは、次のような問題です。原作とは少し表現を変えていますが、実質同じ内容です。

5つのビリヤードの玉を円形に並べる。玉には数字が書いてある。玉をいくつとってもいいが、隣通し連続したものしかとれないとする（離れているものはとれない）。この条件でとった玉の数字を足し合わせて1から21までのすべての数ができるようにするには、ビリヤードの玉をどう並べればいいか

円形ではないですけど、こういうふうに並べるわけです。

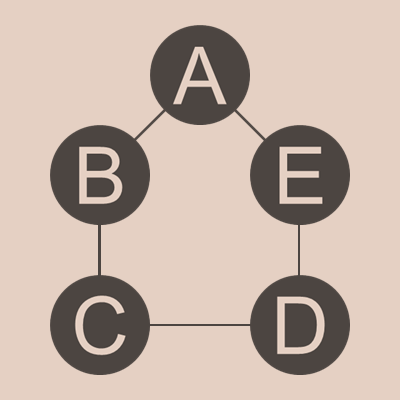
CDとかBAEのように玉を選ぶことはできるけど、CEとかは選べないということですね。10を作るにはABC、15を作るにはCDEみたいな感じで、1から21全てを作れるようにするには、AからEをどうすればいいかということです。

ちなみに、ビリヤードの玉は、1から15まで1個ずつあります。はじめ、1から9までしかないと思い込んでいたので、できないじゃないかと思ってたんですけどね。

さて、どう並べればいいか考えてみましょう。まず、「1」ができないといけないので、1の玉は必ず必要です。円形に並べるので、Aのところを1にして問題ありませんね。

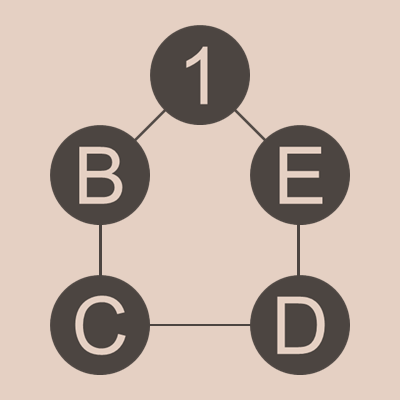
次に、「2」をつくらないといけないので、2の玉も必要です。2は、1の隣に来るか、離れるかの2パターンあります。図で言うと、BかCですね。配置を裏返せばいいので、DはCと同じことだし、EはBと同じことなので、BとCの2パターンを考えれば十分ですね。それぞれの場合を考えていきましょう。

と、その前に、一つ重要なことがあります。そもそも、AからEの足した答えは何個できるか見てみましょう。

数字を1つしか使わない場合は、AからEの5個ですね。2つ使う場合は、A+B、B+C、C+D、D+E、E+Aの5個です。3つの場合も4つの場合もそれぞれ5個ですね。そして、5つ使う場合は、当たり前ですが1個です。つまり全部で21個なわけです。

和の個数が21個あり、これらで1から21まで作らないといけないということから、「どの和も同じになってはいけない」ということがわかります。つまり、「Cが5で、D+Eも5」のような状況になると、和のパターンは21未満になるので、1から21までを作ることができません。この「どの和も同じになってはいけない」というのは、選択肢をしぼっていくのに大変役立ちます。

また、さらに、AからEのすべてを足したこたえは、21になるということも分かります。これも、地味に役立ちます。

1と2が隣り合う場合

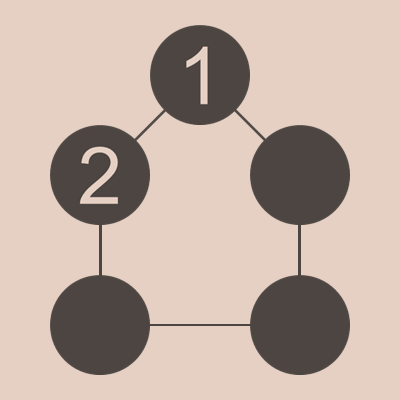
では、まず、1と2が隣り合うパターンから考えてみましょう。「1+2」で3を作ることができるので、3がどこかに入ることはありません。なので次に入る数字は、4ですね。1と2と4が入り、全部の合計が21ということは、他の数字は、(5,9)か(6,8)しかありえません。このことをふまえ、4がどこに入るか考えてみましょう。

4と1が隣り合う場合

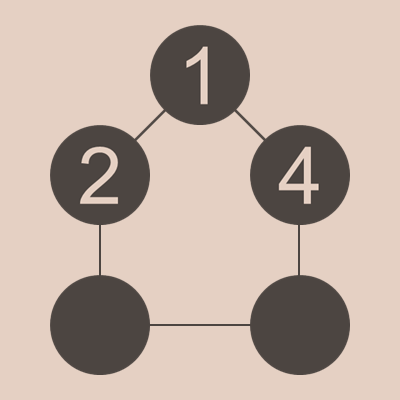
4が1と隣り合う場合、1+4=5が作れるので、残りが(5,9)ということはありえません。なので、(6,8)しか候補はありません。ただ、2の隣りに6がくると、2+6=8となるので、8がダブります。また、2の隣りに8がくると、4の隣が6になり、2+8=10と4+6=10となり、10がダブります。「どの和も同じになってはいけない」ということに反するので、選択肢が全部なくなってしまいました。つまり、この場合は考えられません。

4と2が隣り合う場合

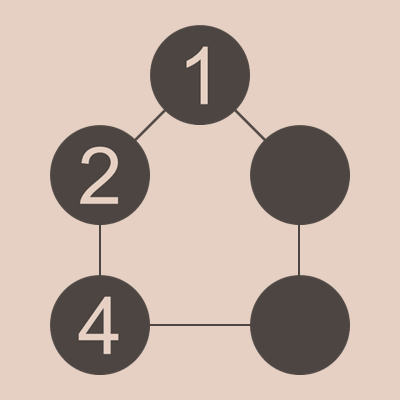
4が2と隣り合う場合、2+4=6が作れるので、残り2つの玉は(5,9)の選択肢しかありません。1の隣に5が来ると、1+5=6と2+4=6となり、6がダブります。1の隣りに9が来ると、4と5が隣り合うことになり、4+5=9と9がダブります。なので、この場合も「どの和も同じになってはいけない」ということに反するため、4と2が隣り合うことがないという結論になります。

4が1とも2とも隣り合わない場合

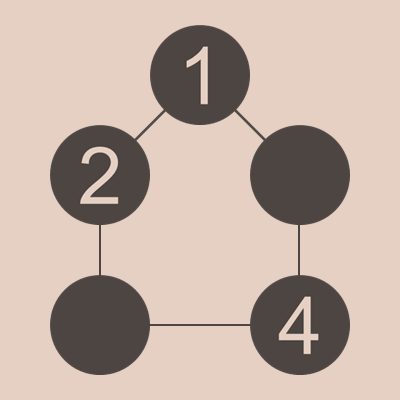
最後は、4が1とも2とも隣り合わない場合、つまり4がDにくるときですね。このとき、1と2と4で5を作ることができないので、残りの2つの玉は(5,9)の選択肢しかありません。しかし、この場合、どちらに5を置いても、4と5は必ず隣り合い、4+5=9と9がダブってしまいます。なので、この場合もあり得ないことがわかります。

以上をまとめると、「1と2が隣り合う場合」は全滅。この場合はどれも条件に当てはまらないということがわかりました。

1と2が隣り合わない場合

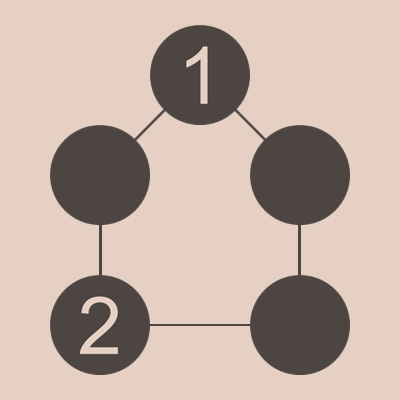
さて、条件を満たすビリヤードの玉の並べ方があり得るとしたら、1と2が隣り合わない場合しかないということがわかりました。このとき、3が作れないので、3がどこかに入るということがわかります。また、5つの玉を足すと21になることから、他の2つの合計は15、つまり、(4,11)、(5,10)、(6,9)、(7,8)の4パターンしかないということがわかります。これを踏まえ、先ほどと同じように、3の場所で場合分けをしてみましょう。

3が1と2の間に来る場合

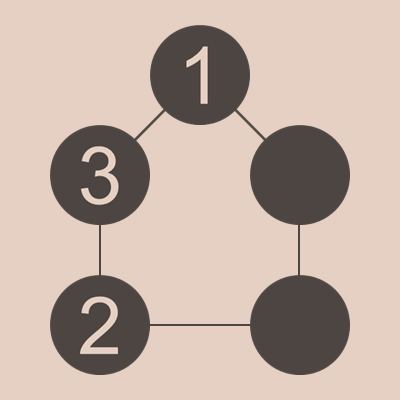
まずは、3が1と2の間に来る場合を考えてみましょう。この場合、この3つの玉で、1から6まで作ることができます。「どの和も同じにならない」ことから考えると、残りの2つは(7,8)のパターンしかないことになります。ただ、1の隣りに7がくると、1+7=8で8がダブるし、1の隣りに8がくると、7は2の隣りになり、1+8=9と2+7=9となってダブってしまいます。なので、3が1と2の間に来ることはない、ということがわかります。

3が2の隣りで1の隣りでない場合

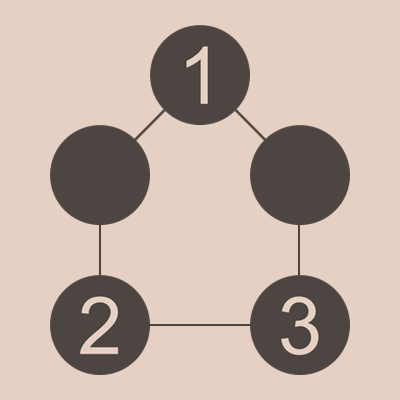
3が2の隣りで1の隣りでない場合、つまり3がDの位置にくる場合は、4が作れないので、残りの2つは(4,11)しかありえません。しかし、どの場合も4と1は隣同士になり、3と2が隣りであることから、1+4=5と2+3=5となってダブってしまいます。なので、この場合もあり得ないことがわかります。

3が1の隣りで2の隣りでない場合

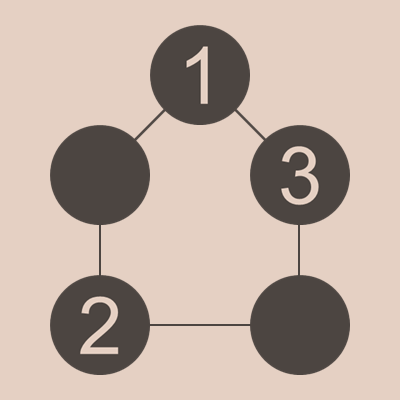
まぁ、もうこの場合しか残っていないわけですが。。。

この場合、5が作れないので、(5,10)の選択肢しかありません。2と3の間に5がくると、2+3+5=10となるため、10がダブってしまいます。なので、あり得ません。

一方、2と3の間に10がくる場合。このとき、配置は次のようになります。

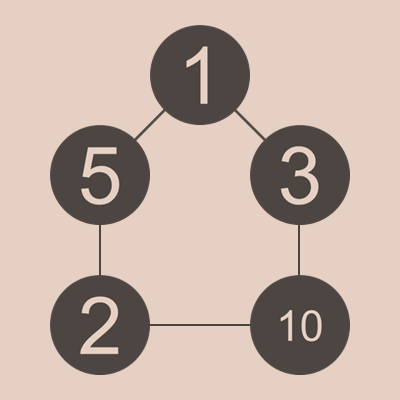
それぞれ式を書いてみます。反時計回りになるように書いています。

1, 2, 3, 4=3+1, 5, 6=1+5, 7=5+2, 8=1+5+2, 9=3+1+5, 10, 11=3+1+5+2, 12=2+10, 13=10+3, 14=10+3+1, 15=2+10+3, 16=2+10+3+1, 17=5+2+10, 18=1+5+2+10, 19=10+3+1+5, 20=5+2+10+3, 21=1+5+2+10+3

なんということでしょう（劇的ビフォーアフター風）。できちゃいました。

まとめ

正直、大変でした。条件が少なくなるように、2つの事実、「どの和も同じになってはいけない」「AからEのすべてを足したこたえは、21になる」を使いましたが、それでも結構めんどうでした。

本では、玉の数が一般の場合はどうなるだろう？　みたいな話が書いてありますが、こんなしらみつぶしの方法では歯が立ちません。もっといい方法があるのだろうか。

前の記事：

[ web ] まともな人はアメブロを去っていく

次の記事：

エクセルで作った画像を、ペイントを使わずに保存する方法